Use Synthetic Division to Solve Mc003-1.jpg. What Is the Quotient?

3.5: Dividing Polynomials

1. Last updated

2. Save as PDF

Page ID

31086

• 
• Primary Lecturer (School of Mathematical and Statistical Sciences) at Arizona Land Academy
• Source: OpenStax CNX

Learning Objectives

• Utilise long sectionalisation to divide polynomials.
• Use synthetic partition to divide polynomials.

Work in Progesss - do not read yet! (maybe have out all worked examples and hand out new ones in form) The exterior of the Lincoln Memorial in Washington, D.C., is a big rectangular solid with length 61.5 meters (thou), width xl m, and summit thirty m.1 We can easily discover the volume using elementary geometry.

\[\begin{marshal*} 5&=l \; {\cdot} \; w \; {\cdot} \; h \\ &=61.v \; {\cdot} \; 40 \; {\cdot} \; 30 \\ &=73,800 \end{marshal*}\]

So the volume is 73,800 cubic meters (\(m^iii\)).

Figure \(\PageIndex{i}\): Lincoln Memorial, Washington, D.C. (credit: Ron Cogswell, Flickr)

Suppose we knew the book, length, and width. Nosotros could split to discover the height.

\[\begin{align*} h&=\dfrac{Five}{50{\cdot}w} \\&=\dfrac{73,800}{61.5{\cdot}40} \\ &=30 \end{align*}\]

As nosotros tin ostend from the dimensions above, the height is thirty thou. Nosotros tin can utilise similar methods to observe whatsoever of the missing dimensions. Nosotros can besides use the same method if whatever or all of the measurements contain variable expressions. For example, suppose the book of a rectangular solid is given by the polynomial \(3x^4−3x^three−33x^2+54x\). The length of the solid is given by \(3x\); the width is given past \(x−2\).

To find the height of the solid, nosotros can employ polynomial division, which is the focus of this section.

Using Long Division to Divide Polynomials

We are familiar with the long division algorithm for ordinary arithmetics. We begin by dividing into the digits of the dividend that have the greatest identify value. Nosotros divide, multiply, subtract, include the digit in the adjacent place value position, and repeat. For example, allow'south carve up 178 by 3 using long division. Needs Work - supercede!

Another way to look at the solution is every bit a sum of parts. This should wait familiar, since it is the aforementioned method used to check segmentation in elementary arithmetic.

\[\begin{align*} \text{dividend}&=(\text{divisor}{\cdot}\text{quotient})+\text{rest} \\ 178&=(three{\cdot}59)+1 \\ &=177+i \\ &=178\end{marshal*}\]

Nosotros telephone call this the Division Algorithm and will discuss it more formally subsequently looking at an example.

Partition of polynomials that incorporate more than than i term has similarities to long division of whole numbers. We can write a polynomial dividend every bit the production of the divisor and the caliber added to the remainder. The terms of the polynomial division correspond to the digits (and place values) of the whole number partition. This method allows the states to divide 2 polynomials. For example, if we were to divide \(2x^three−3x^2+4x+5\) by \(x+two\) using the long sectionalisation algorithm, it would look like this: Needs work - supersede!

Nosotros accept establish

\[\dfrac{2x^3−3x^2+4x+5}{x+2}=2x^2−7x+18−\dfrac{31}{x+2}\]

or

\[2x^iii−3x^2+4x+v=(x+2)(2x^2−7x+18)−31\]

We tin place the dividend, the divisor, the caliber, and the residue.

Writing the consequence in this fashion illustrates the Division Algorithm.

The Division Algorithm

The Division Algorithm states that, given a polynomial dividend \(f(x)\) and a non-zero polynomial divisor \(d(x)\) where the degree of \(d(x)\) is less than or equal to the degree of \(f(ten)\), at that place exist unique polynomials \(q(x)\) and \(r(10)\) such that

\[f(ten)=d(x)q(x)+r(x)\]

\(q(x)\) is the quotient and \(r(x)\) is the residuum. The remainder is either equal to zero or has degree strictly less than \(d(x)\).

If \(r(x)=0\), and so \(d(x)\) divides evenly into \(f(10)\). This means that, in this case, both \(d(ten)\) and \(q(x)\) are factors of \(f(x)\).

Given a polynomial and a binomial, utilize long division to separate the polynomial by the binomial

1. Set up upwards the division problem.
2. Determine the first term of the caliber by dividing the leading term of the dividend by the leading term of the divisor.
3. Multiply the respond by the divisor and write it below the similar terms of the dividend.
4. Subtract the lesser binomial from the tiptop binomial.
5. Bring downwards the adjacent term of the dividend.
6. Echo steps 2–5 until reaching the last term of the dividend.
7. If the remainder is non-zip, express as a fraction using the divisor as the denominator.

Example \(\PageIndex{1}\): Using Long Division to Split a 2d-Degree Polynomial

Dissever \(5x^2+3x−2\) past \(x+ane\). Needs Piece of work - more than space between steps! (replace!)

Solution

The caliber is \(5x−ii\). The remainder is 0. Nosotros write the result as

\[\dfrac{5x^2+3x−2}{ten+i}=5x−2\]

or

\[5x^two+3x−2=(x+1)(5x−2)\]

Analysis

This division problem had a remainder of 0. This tells us that the dividend is divided evenly by the divisor, and that the divisor is a factor of the dividend.

Example \(\PageIndex{2}\): Using Long Division to Divide a Third-Degree Polynomial

Divide \(6x^3+11x^2−31x+15\) by \(3x−2\). Needs work - + sign in line 5 should be a minus!  21x in next line should be -21x! constant term of dividend should be 15! (screen shot)

Solution

In that location is a residuum of one. Nosotros tin can express the upshot as:

\[\dfrac{6x^3+11x^2−31x+15}{3x−2}=2x^two+5x−vii+\dfrac{ane}{3x−two}\]

Analysis

Nosotros can bank check our work past using the Sectionalization Algorithm to rewrite the solution. And so multiply.

\[(3x−2)(2x^2+5x−7)+1=6x^3+11x^2−31x+15\]

Discover, equally nosotros write our effect,

• the dividend is \(6x^3+11x^2−31x+15\)
• the divisor is \(3x−ii\)
• the quotient is \(2x^2+5x−vii\)
• the remainder is \(one\)

\(\PageIndex{2}\)

Divide \(16x^3−12x^2+20x−3\) by \(4x+v\).

Solution

\(4x^ii−8x+15−\dfrac{78}{4x+5}\)

Using Synthetic Sectionalisation to Divide Polynomials

As we've seen, long sectionalization of polynomials can involve many steps and exist quite cumbersome. Synthetic sectionalization is a shorthand method of dividing polynomials for the special case of dividing by a linear factor whose leading coefficient is 1.

To illustrate the process, recall the instance at the get-go of the section.

Divide \(2x^3−3x^two+4x+5\) by \(x+two\) using the long segmentation algorithm.

The concluding form of the process looked like this: Make sure this matches case at beginning of section! (quotient is wrong here)

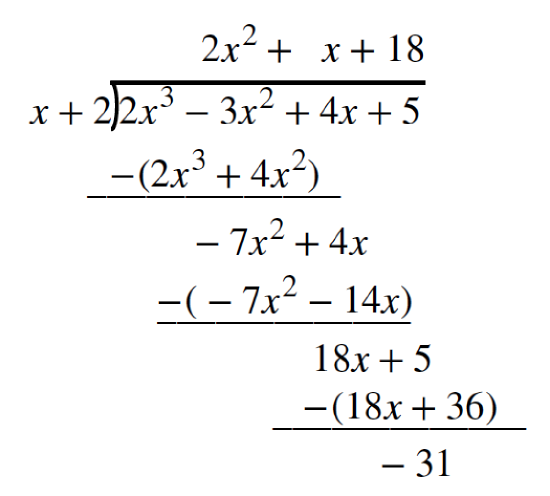
There is a lot of repetition in the table. If we don't write the variables but, instead, line upwards their coefficients in columns under the division sign and also eliminate the partial products, we already have a simpler version of the entire trouble.

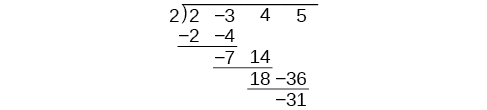
Synthetic sectionalisation carries this simplification even a few more steps. Collapse the table by moving each of the rows up to fill up any vacant spots. Also, instead of dividing by 2, as we would in division of whole numbers, then multiplying and subtracting the heart product, nosotros change the sign of the "divisor" to –ii, multiply and add. The process starts by bringing downwards the leading coefficient.

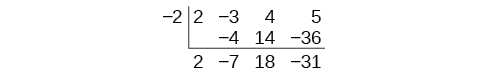
We then multiply information technology by the "divisor" and add, repeating this process column past column, until there are no entries left. The bottom row represents the coefficients of the quotient; the last entry of the lesser row is the remainder. In this instance, the quotient is \(2x^two–7x+18\) and the remainder is –31.The process will be made more clear in Example \(\PageIndex{3}\).

Synthetic Sectionalisation

Constructed division is a shortcut that can exist used when the divisor is a binomial in the form \(10−one thousand\). In synthetic partition, but the coefficients are used in the division process.

Given two polynomials, utilise synthetic sectionalization to divide

1. Write \(1000\) for the divisor.
2. Write the coefficients of the dividend.
3. Bring the lead coefficient down.
4. Multiply the pb coefficient by \(k\). Write the product in the next column.
5. Add the terms of the second cavalcade.
6. Multiply the result by \(k\). Write the product in the next column.
7. Repeat steps 5 and 6 for the remaining columns.
8. Use the bottom numbers to write the quotient. The number in the last column is the residual and has degree 0, the next number from the right has degree 1, the adjacent number from the correct has degree 2, and then on.

Example \(\PageIndex{3}\): Using Synthetic Division to Separate a Second-Caste Polynomial

Use synthetic sectionalization to separate \(5x^2−3x−36\) by \(x−three\).

Solution

Brainstorm by setting upwards the constructed partition. Write \(k\) and the coefficients.

Bring downwards the lead coefficient. Multiply the lead coefficient by \(k\).

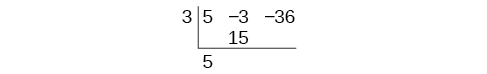
Go on by adding the numbers in the second column. Multiply the resulting number by \(yard\).Write the effect in the side by side column. So add together the numbers in the third column.

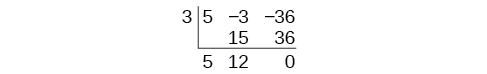
The result is \(5x+12\). The residuum is 0. So \(x−3\) is a factor of the original polynomial.

Analysis

Just equally with long partition, we tin bank check our piece of work by multiplying the quotient past the divisor and calculation the remainder.

\[(ten−3)(5x+12)+0=5x^two−3x−36\]

Example \(\PageIndex{iv}\): Using Synthetic Segmentation to Divide a Third-Degree Polynomial

Use synthetic division to divide \(4x^3+10x^2−6x−20\) by \(10+2\).

Solution

The binomial divisor is \(x+two\) so \(k=−2\). Add each column, multiply the result by –two, and echo until the final column is reached.

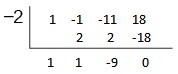
The result is \(4x^two+2x−x\).

The remainder is 0. Thus, \(x+2\) is a factor of \(4x^3+10x^2−6x−20\).

Analysis

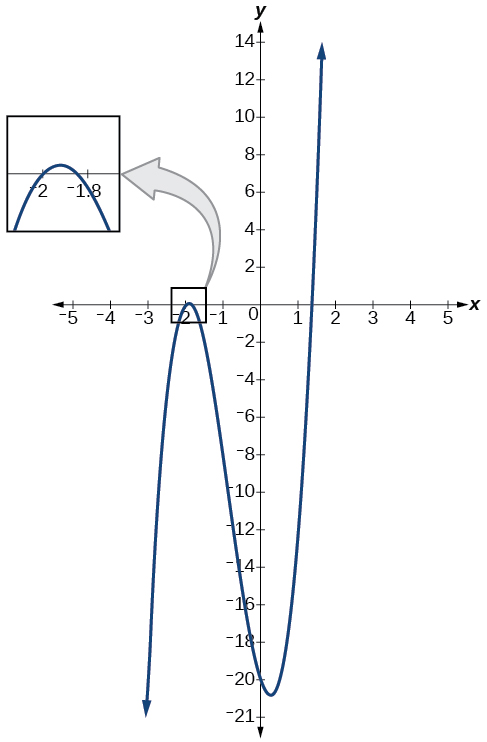
The graph of the polynomial office \(f(x)=4x^three+10x^2−6x−20\) in Figure \(\PageIndex{2}\) shows a nada at \(x=thou=−2\). This confirms that \(x+ii\) is a factor of \(4x^three+10x^two−6x−20\).

Effigy \(\PageIndex{2}\)

Example \(\PageIndex{5}\): Using Synthetic Division to Divide a Fourth-Caste Polynomial

Utilise synthetic division to carve up \(−9x^4+10x^3+7x^2−6\) by \(10−i\).

Solution

Detect there is no x-term. Nosotros will use a zero as the coefficient for that term.

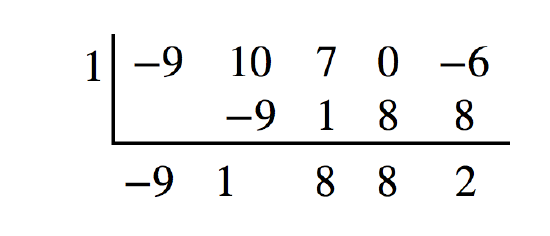
The outcome is \(−9x^three+10^2+8x+8+\frac{2}{x−i}\).

\(\PageIndex{5}\)

Use constructed division to divide \(3x^four+18x^three−3x+40\) past \(10+7\).

Solution

\(3x^three−3x^2+21x−150+\frac{1,090}{x+vii}\)

Using Polynomial Division to Solve Awarding Issues

Polynomial division tin exist used to solve a multifariousness of application problems involving expressions for expanse and volume. We looked at an application at the beginning of this section. Now we volition solve that trouble in the post-obit example.

Example \(\PageIndex{six}\): Using Polynomial Partition in an Awarding Problem

The book of a rectangular solid is given by the polynomial \(3x^iv−3x^three−33x^2+54x\). The length of the solid is given by \(3x\) and the width is given by \(10−two\). Find the meridian of the solid.

Solution

There are a few ways to approach this problem. We need to divide the expression for the volume of the solid by the expressions for the length and width. Allow us create a sketch as in Figure \(\PageIndex{3}\).

Effigy \(\PageIndex{3}\)

Nosotros tin can at present write an equation by substituting the known values into the formula for the book of a rectangular solid.

\[\begin{align*} 5&=l{\cdot}w{\cdot}h \\ 3x^iv−3x^3−33x^2+54x&=3x{\cdot}(10−two){\cdot}h \end{align*}\]

To solve for \(h\), outset divide both sides past \(3x\).

\[\dfrac{3x{\cdot}(x−ii){\cdot}h}{3x}=\dfrac{3x^4−3x^three−33x^ii+54x}{3x}\]

\[(x-2)h=\dfrac{x^3-x^2-11x+xviii}{x-ii}\]

Now solve for \(h\) using synthetic partitioning.

\[h=\dfrac{x^iii−x^ii−11x+18}{ten−two}\]

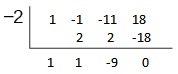
The quotient is \(x^ii+x−9\) and the residual is 0. The height of the solid is \(x^2+x−ix\).

\(\PageIndex{6}\)

The area of a rectangle is given by \(3x^3+14x^2−23x+6\). The width of the rectangle is given by \(x+half-dozen\). Find an expression for the length of the rectangle.

Solution

\(3x^two−4x+i\)

Central Equations

Division Algorithm \(f(x)=d(ten)q(ten)+r(x)\) where \(q(x){\neq}0\)

Key Concepts

• Polynomial long partitioning tin can be used to divide a polynomial by any polynomial with equal or lower degree.
• The Division Algorithm tells u.s.a. that a polynomial dividend tin can exist written as the production of the divisor and the caliber added to the remainder.
• Synthetic division is a shortcut that can be used to split up a polynomial by a binomial in the class 10−one thousand.
• Polynomial division tin can be used to solve awarding problems, including area and book.

Glossary

Sectionalisation Algorithm

given a polynomial dividend \(f(x)\) and a not-naught polynomial divisor \(d(x)\) where the caste of \(d(x)\) is less than or equal to the degree of \(f(x)\), in that location exist unique polynomials \(q(ten)\) and \(r(x)\) such that \(f(ten)=d(x)q(x)+r(x)\) where \(q(10)\) is the quotient and \(r(ten)\) is the remainder. The remainder is either equal to zero or has degree strictly less than \(d(x)\).

constructed division

a shortcut method that can be used to split a polynomial past a binomial of the form \(x−m\)

moransterve87.blogspot.com

Source: https://math.libretexts.org/Courses/Borough_of_Manhattan_Community_College/Professor%27s_Playground/MAT_206.5_Intermediate_Algebra_and_Precalculus_alpha/3:_Polynomial_and_Rational_Functions_New/3.5:_Dividing_Polynomials

Share this post